Segmentación de clientes de un banco con K-Means en R
"NewBank" es una fintech que ha crecido rápidamente en los últimos meses y para mantener este crecimiento necesita identificar estrategias eficientes de comunicación con sus clientes.
Para mantener el anonimato de los datos llamaremos NewBank a nuestro banco, NewBank es una fintech que ha crecido rápidamente en los últimos meses y para mantener este crecimiento necesita identificar estrategias eficientes de comunicación con sus clientes.
Para estructurar este análisis, vamos a utilizar la metodología CRISP-DM, que consiste en:
Entender el negocio.
Entender los datos.
Preparar los datos.
Modelaje estadístico.
Evaluación de resultados.
Implementación del modelo.
1. Entendiendo el negocio
NewBank, ha identificado que sus clientes necesitan productos y beneficios personalizados, de acuerdo a sus necesidades y no desean ser incomodados por ofertas que no se adhieren a sus hábitos y necesidades actuales.
Nuestro reto como científico de datos será estructurar un CRM (Customer Relationship Manager) para el banco.
Los objetivos que deben ser atendidos:
Mejorar el sistema de oferta de nuevos productos y servicios a los clientes.
Subvencionar la creación de programas de fidelización.
Subvencionar la oferta de beneficios exclusivos para clientes especiales.
Monitorear la composición de cartera de clientes.
Un aspecto importante es que, la estrategia a implementar debe ser, de fácil entender para el equipo comercial.
2. Entendiendo la base de datos
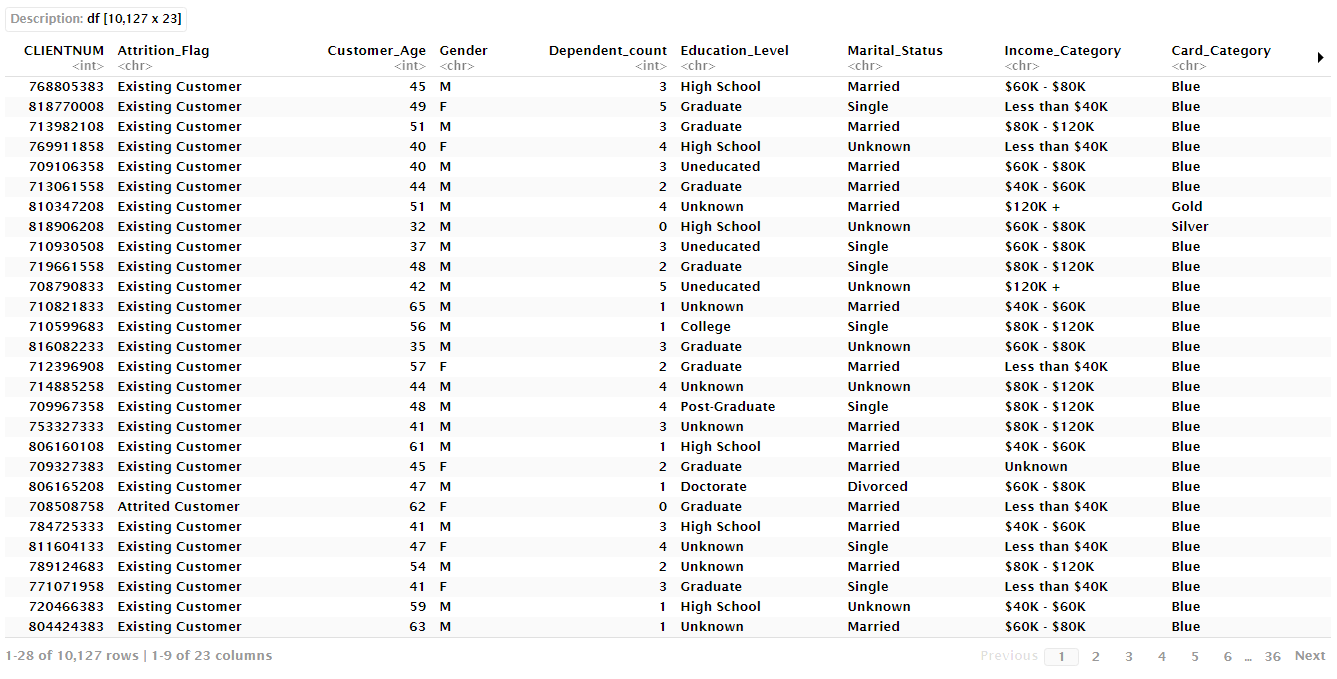
Los datos disponibles contienen información de cerca de 10 mil clientes y se encuentra estructurada de la siguiente manera:
CLIENTNUM: Número de cliente.
Attrition_Flag: Estado de la relación del cliente con el banco.
Customer_Age: Edad del cliente.
Gender: Género del cliente.
Dependent_count: Número de cuentas dependientes que tiene el cliente.
Education_Level: Nivel de educación del cliente.
Marital_Status: Estado civil.
Income_Category: Categoría de ingresos.
Card_Category: Categoría de tarjeta de crédito.
Months_on_book: Número de meses que llevas siendo cliente del banco.
Total_Relationship_Count: Número total de productos.
Months_Inactive_12_mon: Número de meses inactivos en los últimos 12 meses.
Contacts_Count_12_mon: Número de contactos en los últimos 12 meses.
Credit_Limit: Límite de crédito.
Total_Revolving_Bal: Saldo rotatorio total de la tarjeta de crédito
Avg_Open_To_Buy: Línea de crédito promedio.
Total_Amt_Chng_Q4_Q1: Cambio en el monto de la transacción entre Q4 y Q1.
Total_Trans_Amt: Total de transacciones.
Total_Trans_Ct: Importe total de las transacciones.
Total_ct_Chng_Q4_Q1: Cambio en el número total de transacciones entre Q4 y Q1.
Avg_Utilization_Ratio: Índice promedio de uso de tarjetas de crédito.
Es importante tener en cuenta que es una base de datos pequeña con solo 21 variables. Debe verse solo como un ejercicio para ilustrar el proceso de segmentación de clientes.
Comencemos importando la base de datos.
datos <- read.csv("/Bank.csv", header = TRUE)[,-c(22,23)]
datosLibrerías necesarias:
library(tidyr)
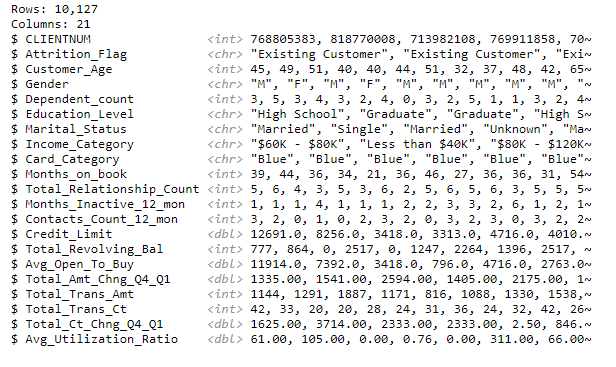
library(dplyr)Inspección inicial de la base de datos utilizando la función glimpse().
glimpse(datos)Es importante tener una idea general de la composición de la base de datos. R ofrece una serie de facilidades para inspeccionar rápidamente el contenido de una base de datos. 'DataExplorer' es particularmente útil en este caso.
library(DataExplorer)
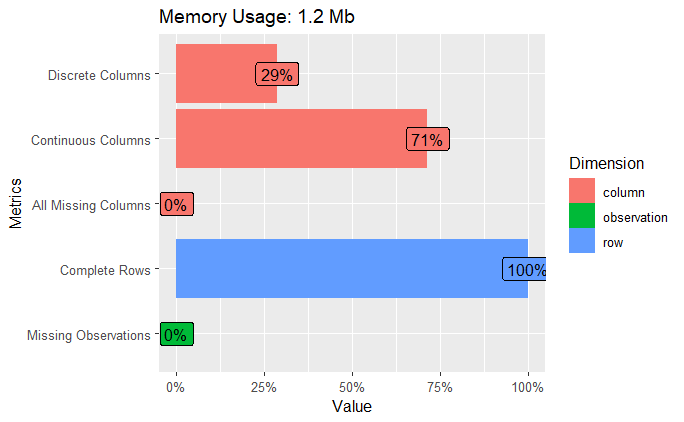
introduce(datos)Otra opción es ver los datos gráficamente.
plot_intro(datos)Nuestro dataset no contienen datos faltantes, tenemos variables continuas y discretas.
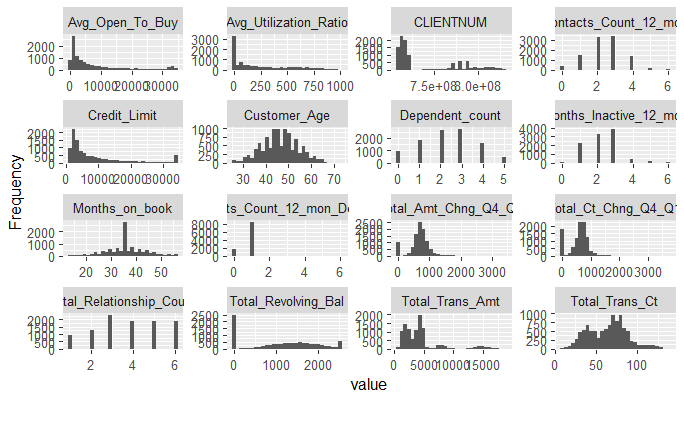
Para los continuos podemos trazar histogramas para evaluar el formato de su distribución.
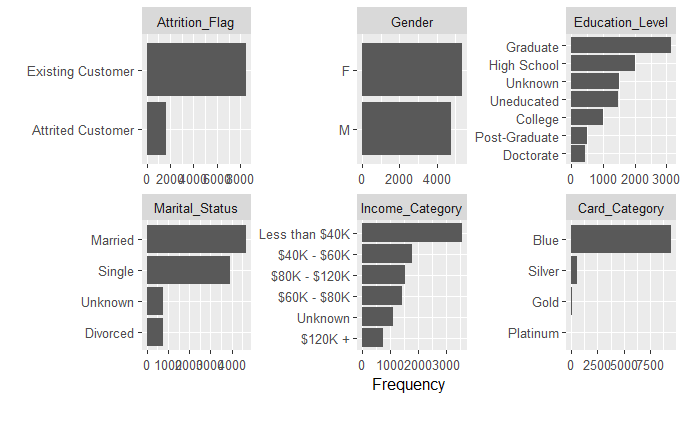
plot_histogram(datos)Por otro lado, para las variables categóricas utilizamos gráficos de barras.
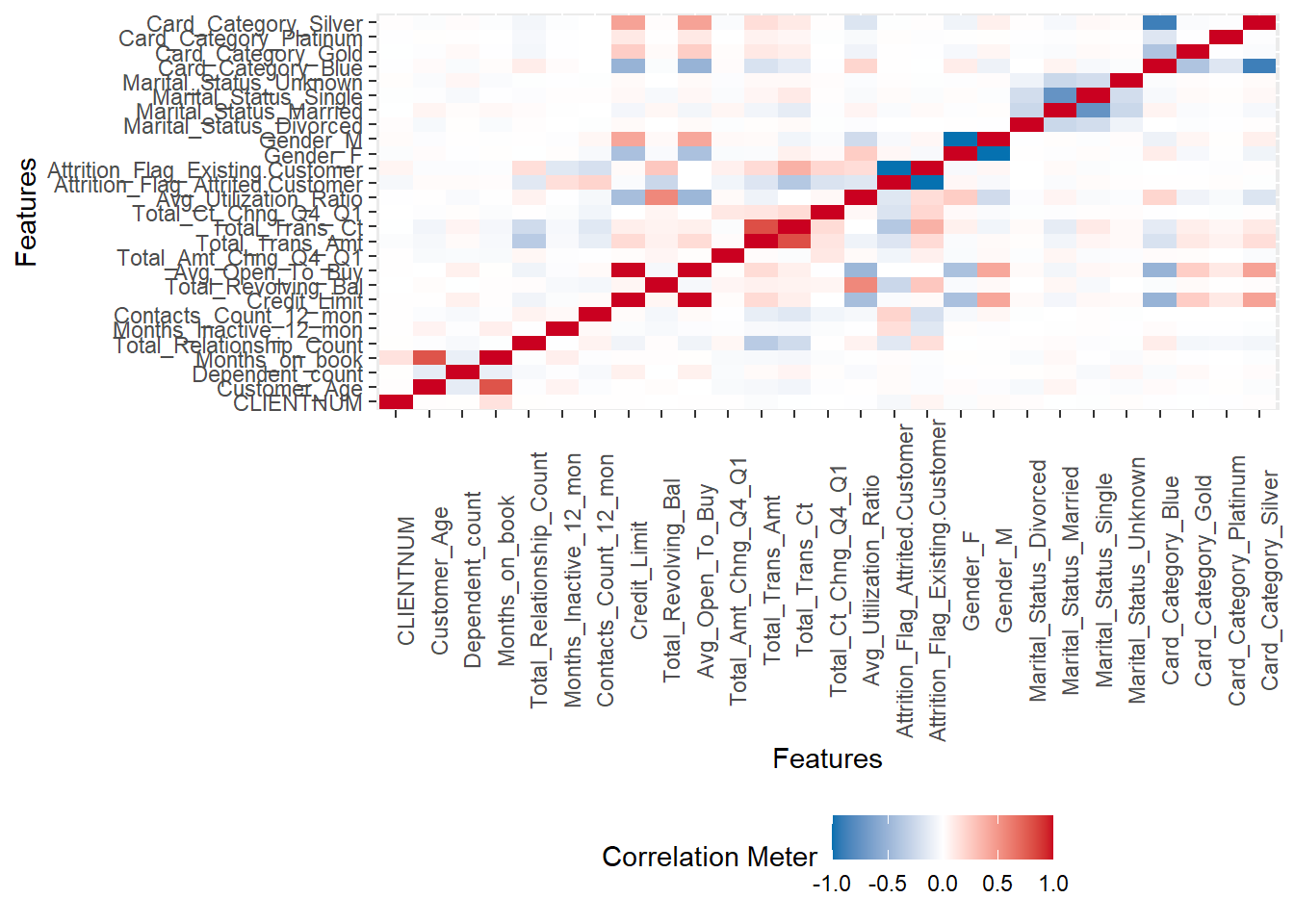
plot_bar(datos)También podemos hacer un análisis de correlación de una manera muy sencilla y ágil.
plot_correlation(na.omit(datos), maxcat = 5L)
## 2 features with more than 5 categories ignored!
## Education_Level: 7 categories
## Income_Category: 6 categoriesPodemos realizar una clusterización utilizando solo covariables que indican el nivel de relación del cliente con NewBank. Por lo tanto, inicialmente descartamos solo para este análisis las variables de registro:
CLIENTNUM: Número de cliente.
Attrition_Flag: Estado de la relación del cliente con el banco.
Customer_Age: Edad del cliente.
Gender: Género del cliente.
Education_Level: Nivel de instrucción del cliente.
Marital_Status: Estado civil.
Otra decisión comercial es que el estado del cliente se puede actualizar mensualmente. Además, también es de interés que el estatus se pueda obtener lo antes posible desde el momento en que el cliente inicia su relación con el banco. Por ello, descartamos algunas variables que necesitan un largo historial de clientes para ser calculadas, son:
Months_Inactive_12_mon: Número de meses inactivos en los últimos 12 meses.
Contacts_Count_12_mon: Número de contactos en los últimos 12 meses.
Total_Amt_Chng_Q4_Q1: Cambio en el monto de la transacción entre Q4 y Q1.
Total_ct_Chng_Q4_Q1: Cambio en el número total de transacciones entre Q4 y Q1.
Avg_Utilization_Ratio: Índice promedio de uso de tarjetas de crédito.
Por último, llegamos al conjunto de datos que se utilizará para construir clustering:
Dependent_count: Número de cuentas dependientes que tiene el cliente.
Income_Category: Categoría de ingresos.
Card_Category: Categoría de tarjeta de crédito.
Months_on_book: Número de meses que es cliente del banco.
Total_Relationship_Count: Número total de productos.
Credit_Limit: Límite de crédito.
Total_Revolving_Bal: Saldo rotatorio total de la tarjeta de crédito.
Avg_Open_To_Buy: Línea de crédito media.
Total_Trans_Amt: Total de transacciones.
Total_Trans_Ct: Importe total de las transacciones.
Es importante destacar que dos de estas variables son categóricas: Dependent_count y Income_category. Por lo tanto, deberán tratarse correctamente para formar parte de la segmentación.
Antes de seguir con el análisis es importante hablar de un término reciente que refleja muy bien cómo los datos son tratados como activos importantes dentro de las empresas “data budget”.
Como vamos a ver la secuencia en la creación de un modelo (un producto basado en datos) existen varias etapas como, estimación de parámetros, selección y mejora de modelos y finalmente la evaluación de su rendimiento. Es importante pensar en cómo se utilizarán los datos en cada una de estas etapas. El término inglés para este paso es "data spending". Parece natural no usar todos nuestros datos en todas las etapas, especialmente cuando uno tiene la intención de validar empíricamente el modelo.
La idea es poder imitar cómo se comportará el modelo en datos que no se utilizaron en ningún momento durante el análisis, imitando en consecuencia lo que sucederá en el mundo real cuando el modelo se ponga en producción.
Este tipo de estrategia es bastante común en la construcción de modelos predictivos. En este ejemplo, trabajaremos con el aprendizaje no supervisado. En esta clase de problemas no tenemos un target para validar nuestro modelo. La validación a menudo se realiza como si la estrategia fuera la adecuada o no adecuada para su uso en el banco, en otras palabras, si la agrupación tiene sentido comercial. Por lo tanto, no utilizaremos ninguna estrategia de partición de datos.
Preparación de datos
El proceso de preparación de datos es muy importante para el éxito de nuestra estrategia analítica. Es importante tener en consideración qué metodología estadística se utilizará en los siguientes pasos y si tiene uno o varios supuestos. En este ejemplo, crearemos una segmentación de clientes. Al principio utilizaremos un método de aprendizaje no supervisado llamado 'kmeans'. de forma bastante simple, el método 'kmeans' busca agrupar a los clientes en grupos que sean lo más homogéneos posible dentro de cada grupo, al tiempo que trata de maximizar la heterogeneidad entre los grupos. La medida que utilizará el algoritmo para medir la homogeneidad es la suma de cuadrados entre los clientes y el centroide (media) del grupo. Para medir qué tan similares son los clientes, el algoritmo utiliza la distancia euclidiana.
Un aspecto importante para los algoritmos basados en la distancia es cuidar la magnitud de las variables. En general, se recomienda que la magnitud de las variables sea similar para que las mediciones de distancia sean comparables, esto puede o no ser importante para un conjunto de datos en particular.
Echemos un vistazo a cómo se ve la magnitud de nuestras variables.
datos <- datos %>%
select(Dependent_count, Income_Category, Card_Category, Months_on_book,
Total_Relationship_Count, Credit_Limit, Total_Revolving_Bal,
Avg_Open_To_Buy, Total_Trans_Amt, Total_Trans_Ct)
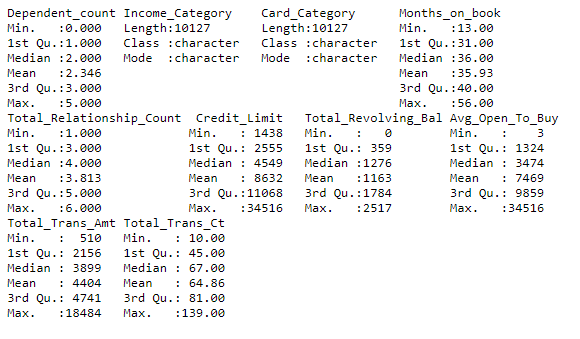
summary(datos)
En este ejemplo tenemos variables de magnitudes o escalas razonablemente diferentes, pero no es una diferencia absurda. Para ejemplificar todos los pasos, normalicemos todas las variables numéricas para que tengan media cero y varianza uno.
Otro aspecto importante es cómo tratar las variables nominales. Para poder considerarlos en el análisis vamos a transformarlas en numéricas, utilizando una estrategia de creación de “dummys”. De forma muy rápida y sencilla creamos varias variables nuevas, indicando si un cliente pertenece (valor 1) o no (valor 0) a una categoría determinada. Por ejemplo, si el cliente tiene ingresos superiores a 120k la variable con ese nombre recibirá uno y todos los demás (con el nombre de los otros niveles de ingresos) recibirá cero.
Otra cuestión es si utilizaremos o no alguna otra transformación que modifique el formato de la distribución de frecuencias. En general, buscamos tratar con variables que tienen una distribución de frecuencia aproximadamente simétrica. Sin embargo, como muestran los histogramas, este no es el caso de las variables que estamos tratando en este análisis. En este ejemplo, elegimos no usar transformaciones que tengan como objetivo cambiar la distribución de frecuencias. En algunos casos, este formato no simétrico puede incluso ser útil para facilitar la división de clientes en grupos. Por ejemplo, la variable 'Total_Revolving_Bal' muestra una alta frecuencia de clientes con el valor 0. Puede ser que solo esta información sea suficiente para crear un grupo de clientes diferente de los demás. La idea es ajustar los 'kmeans' y analizar los resultados.
Un aspecto muy interesante es que todas estas transformaciones se pueden hacer de forma muy sencilla utilizando el paquete `recipes` que compone `tidymodels`.
library(recipes)
ingresos <- recipe(~ ., data = datos) %>%
step_normalize(all_numeric()) %>%
step_dummy(all_nominal())
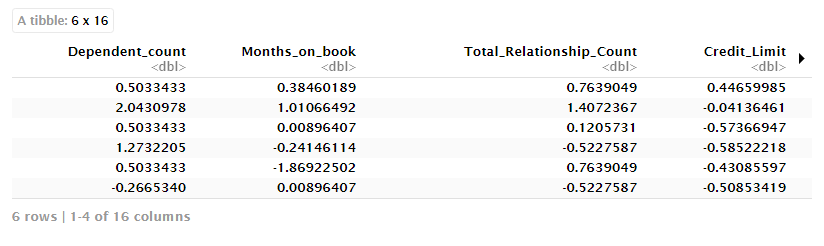
datos_prep <- prep(ingresos)
head(datos_prep$template)Tenemos los datos listos para el siguiente paso que consiste en ajustar el modelo y crear segmentos de clientes. En el caso de los 'kmeans' no se trata exactamente de un modelo estadístico, sino de un algoritmo que pretende agrupar a los clientes.
Modelado estadístico
En cuanto a la elección de la metodología estamos trabajando en una situación de aprendizaje no supervisado. Estamos interesados en dirigirnos a los clientes de NewBank en grupos lo más homogéneos posible.
Entre las diversas estrategias de agrupamiento, el método kmeans es muy popular. A la idea de este método es, dado un vector de características de un cliente, crear grupos donde clientes dentro del mismo grupo, son más parecidos que los clientes en diferentes grupos. Para hacer este agrupamiento, el método kmeans utiliza como medida de resumen de cada grupo la media muestral y el objetivo es hacer que cada cliente pertenezca al grupo con la media más cercana a él. La media de cada grupo corresponde a su centroide e ilustra el comportamiento habitual de un grupo dado.
Para resolver este problema el algoritmo más común utiliza la llamada técnica de refinamiento. La idea es muy simple, dado un conjunto inicial de k means, digamos, μ(1),μ(2),…,μ(k) el algoritmo cambia entre dos pasos:
Paso de agrupación: agrupa cada observación al grupo que tiene la media más cercana en función de alguna medida de distancia, siendo la distancia euclidiana la más común.
Paso de actualización: Recalcula las medias (centroides) dada la agrupación del Paso 1.
El algoritmo se repite hasta que se alcanza algún criterio de parada. Un criterio común es que las observaciones dejen de cambiar de grupo, o equivalentemente, la composición de los grupos no cambie. En general, este algoritmo no tiene convergencia garantizada, pero funciona bien en términos prácticos.
En 'R' la función 'kmeans()' implementa este algoritmo. Para su uso necesitamos la base de datos ya preparada y especificar el número de grupos que se crearán. En este punto, el paquete 'factoextra' es útil para ofrecer una forma sencilla de crear segmentos utilizando diferentes números de grupos y una medida estadística (within sum of squares - wss) para encontrar el número óptimo de grupos.
La elección del número de grupos es un aspecto muy crítico del uso de kmeans. Aunque se dispone de métodos estadísticos, no tienen en cuenta el contexto empresarial en el que se utilizará la técnica. Por ejemplo, si la metodología estadística indica un número muy grande de grupos, puede ser inviable en términos prácticos. En este sentido, de nuevo se deben tener en cuenta criterios prácticos y empresariales.
library(factoextra)
set.seed(123)
muestra <- sample(1:dim(datos)[1], size = 10000)
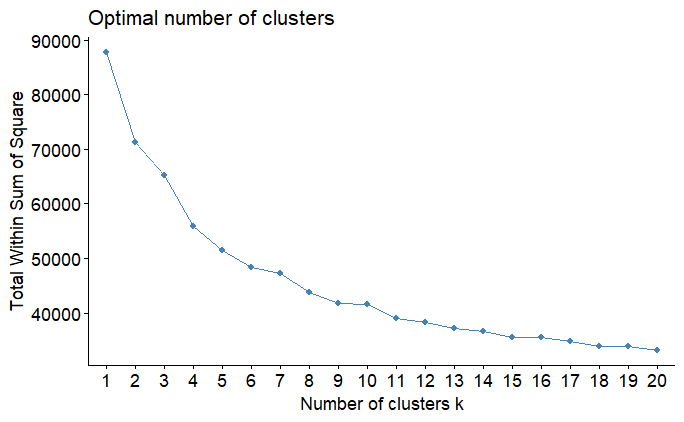
fviz_nbclust(datos_prep$template[muestra,], kmeans, method = "wss", k.max = 20)La figura anterior muestra que la suma de cuadrados decae lentamente incluso a grupos con más de cinco grupos. Este es un comportamiento común cuando aplicamos la técnica a datos que se han normalizado. Debido a que la varianza se estandarizó para ser 1 en todas las variables, esto disminuye la disminución de wss en el gráfico. Puede rehacer el análisis con los datos no estandarizados y verá que alrededor de tres o cuatro grupos es suficiente para que la curva caiga rápidamente.
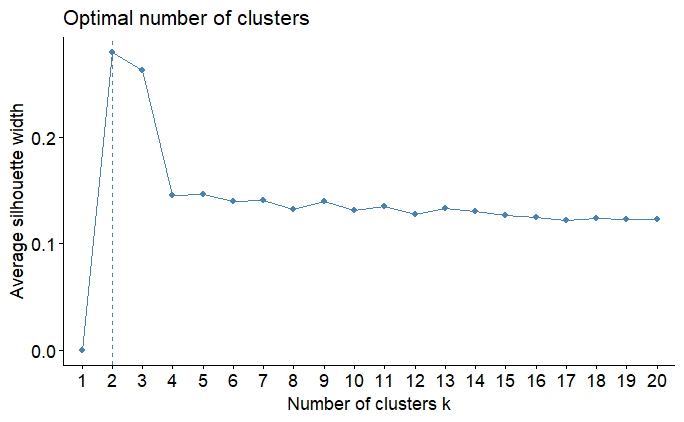
Una técnica más avanzada es el `silhoutte` que se calcula fácilmente, como se muestra en el Código a continuación.
fviz_nbclust(datos_prep$template[muestra,], kmeans, method = "silhouette", k.max = 20)En este caso el número óptimo de segmentos fue de dos, pero teniendo en cuenta los dos wss parece poco, continuemos entonces el análisis con tres segmentos.
Es importante destacar que se deben tener en cuenta tanto los aspectos técnicos como la suma de cuadrados dentro de los grupos, así como los aspectos operativos y de negocio. Un número excesivo de grupos, aunque técnicamente necesario, puede hacer imposible el uso de la segmentación. Para seguir con el ejemplo, obtendremos cinco grupos, pero destacamos que en un análisis posterior es interesante rotar el análisis con más grupos y comparar cualitativamente la calidad de la segmentación creada.
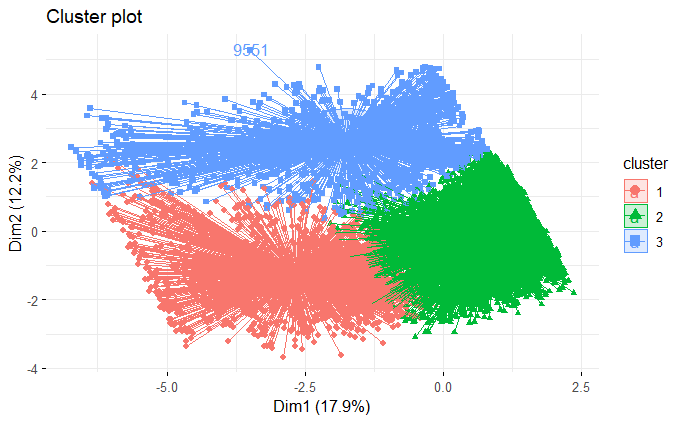
Una forma de visualizar las agrupaciones creadas es utilizar otra técnica de aprendizaje no supervisado para reducir el tamaño del conjunto de datos utilizado en la construcción de la segmentación, y así poder trazar un gráfico en dos dimensiones, donde cada cliente aparece coloreado según el grupo al que fue asignado. Esta técnica se denomina componentes principales. Una vez más, el paquete 'factoextra' ofrece facilidades para este análisis, como se muestra a continuación.
km_res <- kmeans(datos_prep$template, centers = 3, nstart = 25)
fviz_cluster(km_res, data = datos_prep$template, axes = c(1,2),
ellipse.type = "euclid", star.plot = TRUE, repel = TRUE,
ggtheme = theme_minimal())Notamos una superposición razonable entre los grupos, pero solo los dos primeros componentes principales explican solo un poco más del 30% de la variabilidad de la matriz de datos. El último paso es extraer en qué clase se ha designado cada cliente.
datos$cluster <- factor(km_res$cluster)Terminamos así con el uso del algoritmo kmeans. El siguiente paso es evaluar los resultados.
Evaluación de resultados
Con la segmentación creada necesitamos entenderla y evaluar su idoneidad para su uso en la institución. Como tenemos un gran conjunto de variables siendo todavía continuas y categóricas entendiendo lo que hizo la agrupación no es una tarea trivial.
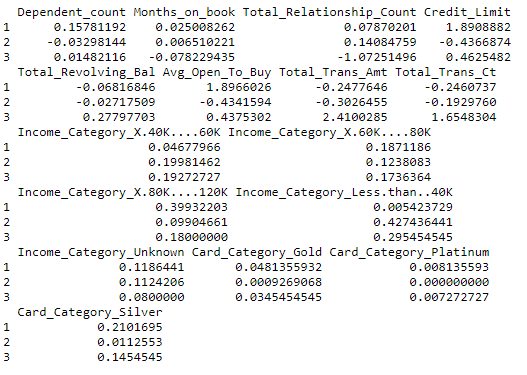
Un primer enfoque es mirar directamente a los centroides de cada grupo.
km_res$centersEn este caso, como las variables se transformaron, es muy difícil tener una interpretación práctica. Podemos obtener los centroides con las variables en la escala original.
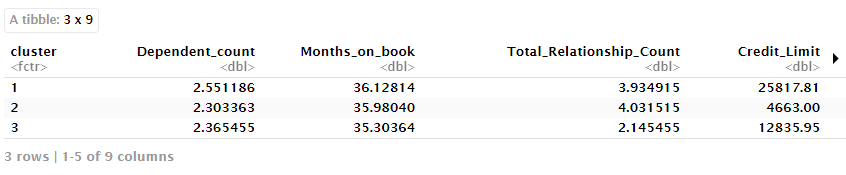
datos %>%
group_by(cluster) %>%
summarise_if(is.numeric, mean, na.rm = TRUE)No hay duda de que se ha vuelto un poco más fácil de interpretar. Sin embargo, para hacerlo aún más fácil podemos utilizar una técnica también del área de machine learning, los árboles de clasificación. La idea es tratar la agrupación creada como target y entender cómo cada variable contribuye a explicar el target, es decir, por qué se asignó a cada cliente en cada grupo. Por lo tanto, también tendremos reglas simples para asignar un cliente en un grupo en particular. Para entrenar nuestro árbol podemos utilizar la sintaxis de 'tidymodels'.
library(tidymodels)
tree_model <-
decision_tree(min_n = 2) %>%
set_engine("rpart") %>%
set_mode("classification")
tree_fit <-
tree_model %>%
fit(cluster ~ ., data = datos)Otra opción es usar la sintaxis a utilizar desde el propio paquete 'rpart'.
library(rpart)
library(rpart.plot)
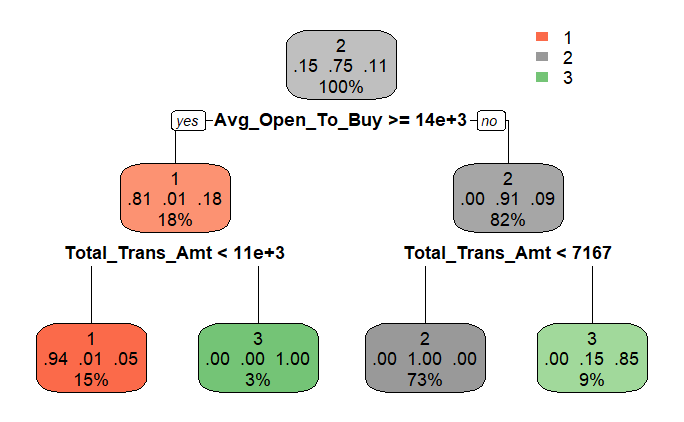
arvore <- rpart(cluster ~ . , cp = .03, data = datos)Una característica muy útil de los árboles es su fácil interpretación gráfica.
rpart.plot(arvore)La ventaja del árbol es proporcionar una forma visual de interpretar cómo se definen los segmentos de acuerdo con las variables utilizadas en la agrupación. Por supuesto, el método no es perfecto, pero ofrece una excelente interpretación de los resultados.
Dichos resultados deben ser evaluados por el equipo de negocio del banco y la evaluación de su idoneidad definida. Obviamente la misma estructura de análisis se puede repetir con otros números de segmento y los resultados comparados para verificar cuál satisface mejor las necesidades del banco.
Implementación del modelo
Finalmente, si el banco considera razonables los segmentos creados, el proceso puede ser enviado a la gerencia y finalmente utilizado para mejorar la comunicación con los clientes. Las estrategias de comunicación con cada tipo de cliente deben ser definidas y posteriormente puestas en práctica.
Otro uso de la estrategia es para un nuevo cliente tan pronto como se disponga de la información necesaria para asignarlo a un segmento.